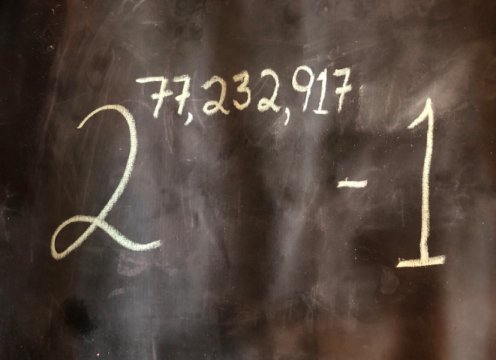Un día después de Navidad, el ingeniero eléctrico Jonathan Pace alcanzó un récord extraño: descubrió el número primo más grande, que contiene más de 23 millones de dígitos.
Pace, de 51 años, ahora es responsable de encontrar el quincuagésimo número de Mersenne y uno de los miles de voluntarios que participan del proyecto The Great Internet Mersenne Prime Search (GIMPS) , o en castellano, La gran búsqueda en Internet del primo de Mersenne.
El nuevo número primo, también conocido como M77232917, tiene casi un millón de dígitos más que el anterior número primo más grande, ahora desplazado del primer puesto. Comienza con 46733318335923109998833 y termina en 1136582730618069762179071.
Dentro del universo de las matemáticas, se encuentra dentro de una categoría “extremadamente rara” de números, conocidos como primos de Mersenne, en honor al sacerdote Marin Mersenne, quien estudió, en el siglo XVII, distintos campos de las matemáticas y la teoría musical.
La prueba de primalidad llevó seis días de verificaciones, y la utilización de cuatro métodos distintos, lo que llevó a la conclusión de que no hay ningún error en M77232917.
El proyecto GIMPS, que utiliza un software gratuito, es responsable de los últimos 16 primos de Mersenne descubiertos.
Pace, que vive en Tennessee, en Estados Unidos, es voluntario del proyecto desde hace más de 14 años y por su descubrimiento, resultó ganador de tres mil dólares. Pero el proyecto continúa: para quien descubra un número primo de cien millones de dígitos, el premio ascenderá hasta los 150 mil dólares de premio, otorgados por la Electronic Frontier Foundation.
NÚMEROS FASCINANTES
En matemáticas, los números primos despiertan la curiosidad tanto de científicos como de amateurs. La definición de un número primo corresponde al número que solo puede ser divido por sí mismo y por 1 para obtener un número entero. Los más conocidos y fáciles de aprender son 2, 3, 5, 7, y 11. El 8, por ejemplo, no es primo porque puede ser dividido por uno, dos, cuatro y ocho.
En el caso de los números primos de Mersenne, estos responden a la fórmula matemática 2P-1. El primer número primo de Mersenne conocido es 3, que surge de la cuenta 22 – 1 = 3.
Los siguientes número primos de Mersenne son 7, 31, y 127, en tanto que la letra P corresponde a 3, 5, y 7 respectivamente.
En el comunicado en donde se anuncia el descubrimiento también se da cuenta de que el estudio de estos números forman parte fundamental de la teoría de números, discutida por primera vez por Euclides en el año 350. El matemático griego demostró que cada primo de Mersenne puede generar, a su vez, un número perfecto. Un ejemplo de esto es el 6. ¿De qué forma? Con una suma: 6=1+2+3. El segundo número perfecto conocido es el 28, que surge a partir de 1+2+4+7+14. El último número perfecto conocido es el resultado de 277,232,916 x (277,232,917-1).
Lejos de ser apenas una atracción matemática, los números de Mersenne son utilizados, por ejemplo, para un sistema de encriptado de Apple. Entre otras aplicaciones, los números primos grandes también sirven para evaluar el rendimiento de chips y otros componentes de las computadoras.